Rôzne spôsoby preukazovania Pythagorovej vety: príklady, popis a recenzie
V jednom si môžete byť istí všetkýmpercentuálne, že k otázke toho, čo sa rovná štvorcu hypotenzie, každá dospelá osoba bude odvážne odpovedať: "Súčet štvorcov nohy". Táto veta sa pevne usadila v mysli všetkých vzdelaných, ale stačí len požiadať niekoho, aby to dokázal, a môžu to byť ťažkosti. Preto si spomeňme a zvážime rôzne spôsoby preukazovania Pythagorovej vety.
Stručný prehľad o biografii
Veta Pythagoras je známa takmer všetkým, alez nejakého dôvodu biografia toho, kto ju vyrobila, nie je tak populárny. To je možné opraviť. Preto pred skúmaním rôznych spôsobov preukazovania Pythagorovho veta by sme sa mali krátko oboznámiť s jeho osobnosťou.

Pythagoras - filozof, matematik, mysliteľ pôvodne zStaroveké Grécko. Dnes je veľmi ťažké rozlíšiť jeho biografiu od legiend, ktoré sa vytvorili v pamäti tohto veľkého človeka. Ale ako vyplýva zo spisov jeho nasledovníkov, Pythagoras of Samos sa narodil na ostrove Samos. Jeho otec bol obyčajný kamenár, ale jeho matka prišla zo šľachtickej rodiny.
Súdiac podľa legendy, vzhľad Pytagorovpredpovedal ženu menom Pythia, na čest ktorej nazvali chlapec. Podľa jej predpovede musel narodený chlapec priniesť mnoho prínosov a dobrého pre ľudstvo. A čo v skutočnosti urobil.
Zrodenie vety
V jeho mladosti sa Pythagoras presťahoval z ostrova Samos do mestaEgypt, stretnúť sa so slávnymi egyptskými mudrcami. Po stretnutí s nimi bol prijatý do štúdia, kde sa naučil všetky veľké úspechy egyptskej filozofie, matematiky a medicíny.
Pravdepodobne sa v Egypte inšpiroval Pythagorasmajestátu a krásy pyramíd a vytvoril svoju veľkú teóriu. To môže šokovať čitateľov, no moderní historici veria, že Pythagoras nedokázal svoju teóriu. Len svoje poznatky postúpil nasledovníkom, ktorí neskôr absolvovali všetky potrebné matematické výpočty.
Čokoľvek to bolo, dnes je známe nielenTechnika dôkazu tejto vety, ale niekoľko. Dnes môžeme len hádať, ako presne starí Gréci urobili svoje výpočty, takže tu zvažujeme rôzne spôsoby dokázania Pythagorovej vety.
Pytagorovská veta
Pred začatím výpočtov musíte zistiť, ktorá teória dokáže. Pythagorovu vetu sa zní takto: "V trojuholníku s jedným z uhlov rovné 90o, súčet štvorcov končatín sa rovná štvorcu hypotenze. "
Celkovo existuje 15 rôznych spôsobov, ako dokázať Pythagorovu vetu. Je to pomerne veľká postava, takže dávajte pozor na najpopulárnejšie z nich.
Metóda jedna
Po prvé, označíme, čo nám bolo dané. Tieto údaje budú rozšírené aj na iné metódy dôkazu Pytagorovskej vety, takže stojí za to pamätať všetky dostupné notácie.
Predpokladajme, že pri obdĺžnikovom trojuholníku, s nohami a, b a hypotenuse, sa rovná c. Prvý spôsob dokazovania je založený na skutočnosti, že obdĺžnik musí nakresliť štvorec.
Aby ste to dosiahli, potrebujete dĺžku anakresliť segment rovný katete a naopak. Toto má viesť k dvom rovnakým stranám štvorca. Zostáva len kresliť dve paralelné priamky a štvorec je pripravený.

Vo výslednom čísle musíte nakresliť viacjeden štvorec so stranou rovnou hypotenzii pôvodného trojuholníka. Aby ste to urobili, z vrcholov ac a st musia vykresliť dva paralelné segmenty s rovnakým c. Získame tak tri strany námestia, z ktorých jedna je hypotenzou pôvodného obdĺžnikového trojuholníka. Zostáva len dotovať štvrtý segment.
Na základe výsledného čísla môžeme konštatovať, že plocha vonkajšieho štvorca je (a + b)2, Ak sa pozriete do obrázku, môžete vidieť, že okrem vnútorného námestia sú v ňom štyri obdĺžnikové trojuholníky. Plocha každej z nich je 0,5 aV.
Preto je plocha: 4 * 0,5av + s2= 2ав + с2
Preto (a + b)2= 2ав + с2
A následne s2= a2+ v2
Veta je preukázaná.
Metóda 2: podobné trojuholníky
Tento vzorec pre dôkaz vetu Pythagorasbol odvodený na základe vyhlásenia z geometrickej časti o podobných trojuholníkoch. Hovorí sa, že katet pravého trojuholníka je priemerne proporcionálny svojou hypotenézou a segmentom hypotenze vychádzajúcej z vrcholu rohu 90o.
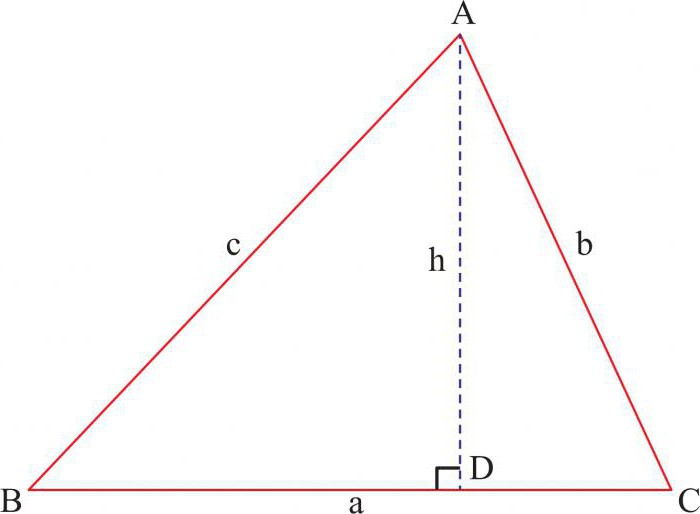
Počiatočné údaje zostávajú rovnaké, a preto začneme ihneď s dôkazom. Na segment AB sme nakreslili kolmo na segment SD. Na základe vyššie uvedeného výroku sú trojuholníkové nohy:
AC = √AB * AD, CB = √AB * DV.
Aby sme odpovedali na otázku, ako dokázať Pythagorovu vetu, dôkaz musí byť vytvorený rozdelením obidvoch nerovností.
AS2= AB * AD a CB2= AB * DV
Teraz musíme doplniť výsledné nerovnosti.
AS2+ CB2= AB * (АД * ДВ), kde АД + ДВ = АВ
Ukazuje sa, že:
AS2+ CB2= AB * AB
A následne:
AS2+ CB2= AB2
Dôkaz o Pythagorovej vetve a rôzne metódy na jej riešenie si vyžadujú všestranný prístup k tomuto problému. Táto možnosť je však jedna z najjednoduchších.
Ďalšia metóda výpočtu
Popis rôznych spôsobov dokazovania vetyPytagoras nemôže povedať nič, až kým nebudete začať cvičit. Mnoho metód poskytuje nielen matematické výpočty, ale aj konštrukciu nových čísel z pôvodného trojuholníka.
V tomto prípade je potrebné doplniť ďalší obdĺžnikový trojuholník VSD z BC. Teraz teda existujú dva trojuholníky s bežnou nohou BC.
Keď vieme, že oblasti s podobnými údajmi majú pomer ako štvorce ich podobných lineárnych rozmerov, potom:
SABC * s2- SAVD* v2 = SAVD* a2- SIRR* a2
SABC* (s2-v2) = a2* (S.AVD-SIRR)
s2-v2= a2
s2= a2+ v2
Keďže z rôznych metód dokazovania Pythagorovej vety pre stupeň 8 je tento variant ťažko vhodný, je možné použiť nasledujúci postup.
Najjednoduchší spôsob, ako preukázať vetu Pythagoras. recenzia
Ako historici veria, táto metóda bola prvýkrátpoužitý na dokázanie vety aj v starovekom Grécku. Je to najjednoduchšie, pretože nevyžaduje absolútne žiadne výpočty. Ak je výkres nakreslený správne, potom dôkaz o tvrdení, že a2+ v2= s2 , bude vidieť jasne.
Podmienky pre túto metódu budú mierne odlišné od predchádzajúcej. Aby sme preukázali vetu, predpokladajme, že pravý trojuholník ABC je rovnoramenný trojuholník.
Vzťahujeme hypotenzu AS na stranu štvorca adcéry tri zo svojich strán. Navyše je potrebné nakresliť dve diagonálne čiary na výslednom štvorci. Tak, získať v ňom štyri rovnoramenné trojuholníky.
K nohám AB a CB musíte tiež mať dieťa na námestí a nakreslite jednu diagonálnu čiaru v každom z nich. Prvý riadok sa čerpá z vrcholu A, druhý je vykreslený z C.

Teraz sa musíte pozrieť na výsledný výkres. Keďže na hypotenze AS sú štyri trojuholníky, ktoré sa rovnajú pôvodnému trojuholníku a na dvoch nohách, naznačuje to pravdivosť vety.
Mimochodom, vďaka tejto metóde dokazovania Pythagorovej vety sa objavila slávna fráza: "Pytagorské nohavice sú rovnaké vo všetkých smeroch".
Dôkaz o G. Garfielde
James Garfield je dvadsiatym prezidentom Spojených štátov amerických. Okrem toho opustil svoju históriu v histórii ako vládca Spojených štátov, bol tiež nadaný samouk.
Na začiatku svojej kariéry bol obyčajnýučiteľka vo verejnej škole, ale čoskoro sa stala riaditeľkou jednej z vyšších vzdelávacích inštitúcií. Túžba po vlastnom rozvoji mu umožnila navrhnúť novú teóriu o dôkazoch Pythagorovej vety. Veta a príklad jej riešenia sú nasledovné.
Najprv musíte nakresliť list papiera dvaobdĺžnikový trojuholník takým spôsobom, že katet jedného z nich je pokračovaním druhého. Vrcholy týchto trojúhelníkov musia byť pripojené tak, aby sa trapezium nakoniec ukázalo.
Ako je známe, plocha lichobežníka sa rovná súčinu polovice súčtu jeho základov k výške.
S = a + b / 2 * (a + b)
Ak vezmeme do úvahy výsledný lichobežník ako obrázok pozostávajúci z troch trojuholníkov, potom jeho plocha môže byť nájdená takto:
S = av / 2 * 2 + s2/ 2
Teraz je potrebné vyrovnať dva počiatočné výrazy
2ab / 2 + c / 2 = (a + v)2/ 2
s2= a2+ v2
Veta o Pythagoras a metódy jej dôkazu možno napísať nielen v jednom zväzku učebnice. Má však v ňom nejaký zmysel, keď sa tieto vedomosti nemôžu uplatniť v praxi?
Praktická aplikácia Pythagorovej vety
Bohužiaľ, v moderných školských osnováchTáto veta je určená len na geometrické problémy. Absolventi čoskoro opustia školské múry bez toho, aby vedeli, a ako môžu uplatniť svoje vedomosti a zručnosti v praxi.
V skutočnosti používať Pythagorovu vetuKaždý ich môže robiť každý deň. A nielen v profesionálnej práci, ale aj v bežných domácich záležitostiach. Pozrime sa na niekoľko prípadov, keď sa Pytagorovská veta a metódy jej dôkazu môžu ukázať ako veľmi nevyhnutné.
Spojenie medzi vetou a astronómiou
Zdá sa, ako môžu byť hviezdy a trojuholníky spojené na papieri. V skutočnosti je astronómia vedeckou oblasťou, v ktorej je široko používaná Pythagoreanova veta.
Zvážte napríklad pohyb svetelného lúča v priestore. Je známe, že svetlo sa pohybuje v oboch smeroch pri rovnakej rýchlosti. Trajektória AB, ktorá pohybuje lúčom svetla, sa nazýva l. A polovica času, kedy sa svetlo musí dostať z bodu A do bodu B, budeme nazývať T, A rýchlosť lúča - C. Ukazuje sa, že: c * t = 1

Ak sa pozrieme na tento lúč z inéhonapr. z vesmírnej vložky, ktorá sa pohybuje s rýchlosťou v, potom s takým pozorovaním telies sa ich rýchlosť zmení. V tomto prípade sa aj pevné prvky pohybujú v rýchlosti v opačným smerom.
Povedzme, že komiksová plavák pláva doprava. Potom sa body A a B, ktorá je roztrhaný medzi nosníka sa bude pohybovať doľava. Okrem toho, keď sa lúč pohybuje z A do B, bod A čas na prechod, a v súlade s tým Svetlo prišlo do nového bodu C. Pre zistenie polovicu vzdialenosti, pri ktorej je bod A sa pohybuje, je potrebné znásobiť rýchlosť lode v polčase lúč jazdy (t ").
d = t "* v
Ak chcete nájsť vzdialenosť, ktorú by mohol prejsť lúč svetla počas tejto doby, musíte označiť polovicu cesty nového buka a získať nasledujúci výraz:
s = c * t "
Ak si predstavujete, že body svetla sú C a B, aKeďže priestorová vrstva je vrcholom rovnoramenného trojuholníka, segment od bodu A do vložky ho rozdelí na dva pravé trojuholníky. Preto vďaka Pythagorovej vetve môžete nájsť vzdialenosť, ktorú by mohol prejsť lúč svetla.
s2 = l2 + d2
Tento príklad, samozrejme, nie je najúspešnejší, pretože len málo z nich môže mať to šťastie, aby to skúsilo v praxi. Z tohto dôvodu považujeme za svetlejšie varianty aplikácie tejto vety.
Mobilný signálový rádius
Moderný život už nemožno predstaviť bez existencie smartfónov. Ale koľko by z nich bolo, keby nemohli spojiť účastníkov prostredníctvom mobilnej komunikácie?
Kvalita mobilnej komunikácie priamo závisívýška antény mobilného operátora. Ak chcete vypočítať, ako ďaleko môže telefón prijímať signál z mobilnej veže, môžete použiť Pythagorovu vetu.
Predpokladajme, že musíte nájsť približnú výšku pevnej veže tak, aby mohla šíriť signál v okruhu 200 kilometrov.
AB (výška veže) = x;
SU (rádius prenosu signálu) = 200 km;
OS (polomer zemeguľa) = 6380 km;
Odtiaľto
OB = OA + ABOV = r + x
Pri použití Pythagorovej vety zistíme, že minimálna výška veže by mala byť 2,3 km.

Pythagoreanova veta v každodennom živote
Zdá sa, že Pythagoreanova veta môže byťužitočné aj v domácich záležitostiach, ako napríklad stanovenie výšky skrine. Na prvý pohľad nie je potrebné používať takéto zložité výpočty, pretože jednoducho môžete robiť merania pomocou rulety. Mnohí sa však opýtali, prečo sú v montážnom procese určité problémy, ak boli všetky merania vykonané viac než presne.
Skutočnosťou je, že šatník sa chystáv horizontálnej polohe a len potom stúpa a inštaluje sa proti stenu. Preto v procese zdvíhania konštrukcie by mala bočná stena skrine voľne prejsť tak pozdĺž výšky, ako aj diagonálne v miestnosti.
Predpokladajme, že je tu šatník s hĺbkou 800 mm. Vzdialenosť od podlahy k stropu je 2600 mm. Skúsený výrobca nábytku povedie, že výška skrinky by mala byť o 126 mm menšia ako výška miestnosti. Ale prečo presne 126 mm? Zvážte príklad.
S ideálnymi rozmermi skrinky skontrolujte efekt Pythagorovej vety:
AC = √AB2+ √ВС2
AC = √24742+8002= 2600 mm - všetko sa hodí.
Predpokladajme, že výška skrine nie je rovná 2474 mm, ale 2505 mm. potom:
AC = √25052+ √8002= 2629 mm.
V dôsledku toho nie je táto skrinka vhodná na inštaláciu v tejto miestnosti. Keď ho zdvíhate vo vertikálnej polohe, môžete poškodiť jeho telo.

Možno, keď zvážili rôzne spôsoby dokazovaniaPythagoreanské vety od rôznych vedcov, môžeme konštatovať, že je viac ako pravda. Teraz môžete použiť informácie získané v každodennom živote a byť úplne istí, že všetky výpočty budú nielen užitočné, ale aj pravdivé.




